BranchOut heeft de laatste tijd zeer veel publiciteit (ook hier op RecruitmentMatters) weten te genereren als gevolg van hun astronomische groei. Ter illustratie; een maand geleden stond het gemiddeld aantal maandelijkse gebruikers bij BranchOut op 4 miljoen, vandaag staat dat aantal op 9,3 miljoen. Inderdaad; een groei van 5,3 miljoen in slechts 31 dagen. Wat tot allerhande speculaties leidt dat BranchOut een tipping point heeft bereikt, dat BranchOut binnenkort LinkedIn naar de kroon gaat steken, etc.

Helaas zijn deze speculaties uitsluitend gebaseerd op aantallen gebruikers en niet op de feitelijke waarde die BranchOut al dan niet biedt aan diezelfde gebruikers. Daarom leek het me leuk om hier een speculatie tegenover te stellen; waarbij ik er niet vanuit ga dat BranchOut een tipping point heeft bereikt maar dat BranchOut een piramidespel is. Of zoals de Amerikanen zo fraai zeggen: a ponzi scheme.

Waarom zou BranchOut een piramidespel zijn? Nou, die kans is redelijk groot als gevolg van het aanmeldingsproces dat BranchOut hanteert. Waarbij de Facebook app een stap in dat proces heeft zitten waar je al je Facebook connecties (tot een door Facebook ingesteld maximum van 50) kan uitnodigen om zich te registreren bij BranchOut.

Even lekker rekenen
Als gedachtenexperiment heb ik daarom eens gekeken of ik een berekening kon maken die de groei in beeld kon brengen op basis van die stap in het aanmeldingsproces. Waarbij ik de volgende criteria heb gehanteerd:

• Ieder nieuwe BranchOut gebruiker die zich aanmeldt stuurt gemiddeld 25 e-mail naar zijn/haar Facebook connecties.
• Van de 25 Facebook connecties die deze e-mail ontvangen, meldt zich iets meer dan 1 connectie zich bij BranchOut aan. Om precies te zijn; ik heb hiervoor het getal van 1,098 connecties gebruikt. Waarmee ik dus fractioneel boven een lineaire groei (van 1) ga zitten.
• Een dag nadat 25 Facebook connecties een e-mail ontvangt, meldt 1,098 connecties zich aan bij BranchOut.
• Vanaf de dag na de aanmelding wordt BranchOut niet meer bezocht door de aangemelde connecties.
• Er kunnen maximaal zoveel e-mails worden verzonden als er Facebook leden zijn; na 1 miljard verzonden e-mails stopt het proces van uitnodigen. Dit zou een soort ideale wereld veronderstellen waarin iedere Facebook gebruiker maximaal 1 BranchOut uitnodiging ontvangt. Geen realistisch scenario, maar op zijn minst een astronomisch volume aan e-mails…

En dat leidt tot de volgende grafiek:

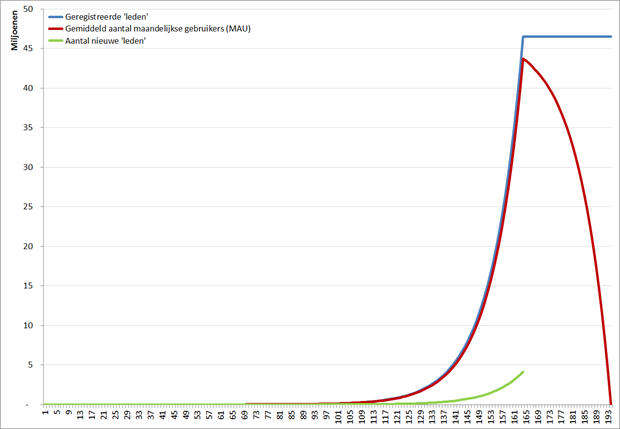
Berekening groei aantal nieuwe ‘leden’, gemiddeld aantal maandelijkse gebruikers en totaal aantal ‘leden’

Herkent iemand een piramidevorm…?

Wat direct opvalt is de bekende situatie bij exponentiele groei, een zeer lange aanloop met een initieel zeer trage maar zich steeds verder versnellende groei. Exponentieel dus. Waarbij ik naast het aantal leden ook het gemiddeld aantal maandelijkse gebruikers (MAU) laat zien; de rekeneenheid die door Facebook en AppData wordt gebruikt om de omvang van een bepaalde Facebook applicatie te tonen. En zoals duidelijk wordt is in een situatie van exponentiele groei de MAU slechts een fractie lager dan het aantal geregistreerde leden. Hierbij heb ik aangenomen dat de dag na een aanmelding een gebruiker niets meer met de applicatie doet.

De piek van het aantal geregistreerde ‘leden’ ligt bij het bereiken van die grens van 1 miljard verzonden e-mails. Dat gebeurt overigens op de dag dat er ruim 94 miljoen uitnodigingen verzonden worden per e-mail… Op dat moment bereikt het aantal geregistreerde ‘leden ‘ haar piek: ruim 46 miljoen, en de groei in het aantal nieuwe ‘leden’ op een dag is dan ook het hoogst; ruim 4 miljoen. Maar op basis van het ontbreken van enige activiteit binnen BranchOut is de neergang nog veel sneller; binnen een maand is BranchOut een doodstille woestijn geworden.

Maar hoe zit het met BranchOut?
Deze extreme vereenvoudiging van de werkelijkheid is niet meer dan een verbeelding van hoe een piramidespel werkt. Bij een tipping point is er een snellere groei van het aantal leden, maar vooral een toename van de activiteit binnen de applicatie. En vooral dat laatste lijkt ten enen  male bij BranchOut te ontbreken.

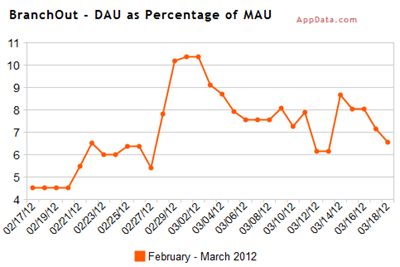
Want dit is de AppData grafiek van de laatste maand van het percentage aan dagelijkse gebruikers  (DAU) ten opzichte van het aantal maandelijkse gebruikers (MAU) binnen BranchOut:

Daily average users as a percentage of monthly average users bij BranchOut. Bron: AppData

Bovenstaande grafiek lijkt een forse hoeveelheid activiteit binnen de applicatie te suggereren; met percentages tussen de 5% en 11% van het aantal maandelijkse gebruikers die dagelijks ‘iets’ doen binnen BranchOut. Maar is dat ook daadwerkelijk een forse activiteit? Het antwoord is: Nee.

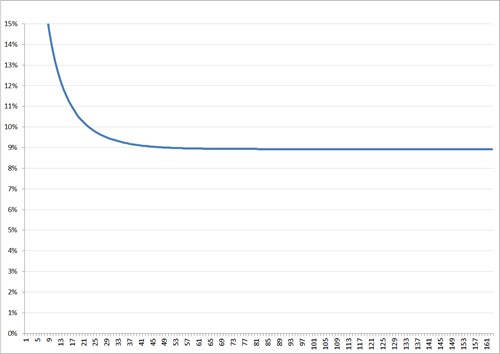
Tenminste, als het eerdere rekenmodel enig houvast biedt. Want op basis van het rekenmodel is vast te stellen dat bij de gekozen exponentiele groei van aanmeldingen (als enige activiteit binnen de applicatie) er een dagelijkse activiteit (DAU) van minimaal 8,9% te verwachten is…:

Daily average users as a percentage of monthly average users op basis van het rekenmodel

Inderdaad, met een DAU van bijna 9% binnen het rekenmodel gebeurt er niets anders dan enige activiteit op de dag van de aanmelding van een gebruiker. Daarna komt de gebruiker nooit meer terug. Maar door de exponentiele groei lijkt het alsof er een behoorlijke activiteit binnen de applicatie is. Het tegendeel is echter waar.

Gezien de cijfers van BranchOut (exponentiele groei, lage DAU als percentage van MAU) lijkt het er dus ernstig op dat BranchOut een piramidespel is en niets meer dan dat. Maar hoelang gaat het nog duren voordat dit duidelijk wordt? Nou, de wereld gedraagt zich niet naar de aannames van een rekenmodel, maar op enig moment is ook voor BranchOut de koek op. Dan is iedere Facebook gebruiker tientallen tot honderden keren benaderd met uitnodigingen die en masse genegeerd haan worden waardoor de ratio onder de 1 (diezelfde ratio waarbij ik 1,098 heb gebruikt) zakt. En als dat gebeurt stort de piramide met donderend geraas in elkaar.

Opkomst en ondergang van een piramidespel
Wanneer dat gaat gebeuren? Geen idee. Maar laat ik daarvoor het rekenmodel eens oprekken. En niet abrupt stoppen als er 1 miljard e-mails zijn verzonden. Maar uitsluitend vanaf dat moment de ratio van 1,098 veranderen in 0,98. Dus fractioneel lager dan 1, waardoor er zich ‘slechts’ 0,98 Facebook connecties zich bij BranchOut aanmelden op basis van 1 eerdere aanmelding (met 25 e-mail uitnodigingen). En dat vanaf dat moment de ‘wet’ van de verminderde meeropbrengst gaat spelen (door met elke volgende stap 0,001 van dat getal van 0,98 af te trekken). Wat gebeurt er dan?

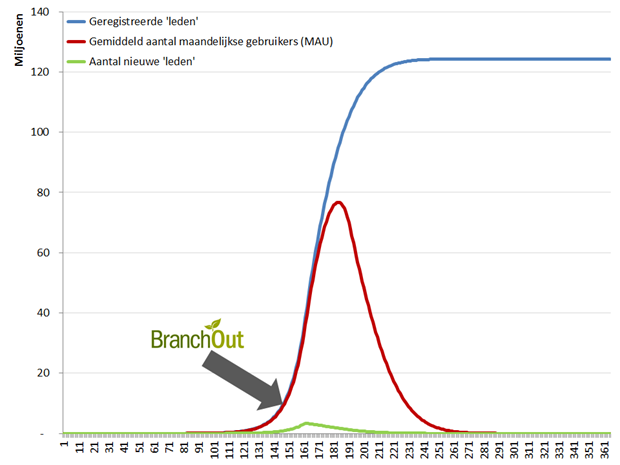
Nou, dit. Waarbij ik ook even de huidige positie van BranchOut heb aangegeven:

Berekening groei aantal nieuwe ‘leden’, gemiddeld aantal maandelijkse gebruikers en totaal aantal ‘leden’

Best wel een indrukwekkend beeld. Het aantal ‘leden’ kan astronomisch hoog worden zonder dat het ook maar iets voorstelt. Maar goed, dat is ook de definitie van een piramidespel.

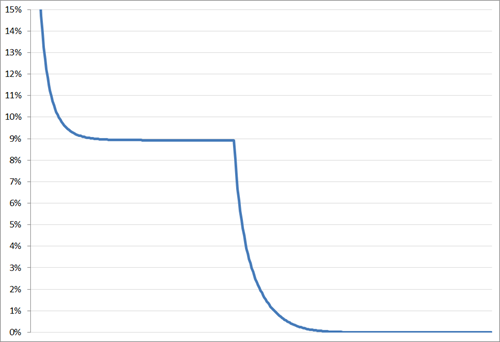
Overigens zullen de eerste tekenen van de ineenstorting zich tonen in de daling van de dagelijkse activiteit als percentage van de maandelijkse activiteit:

Daily average users as a percentage of monthly average users op basis van het rekenmodel

Inderdaad, dat percentage stort zeer snel in om vervolgens geleidelijk richting 0% af te glijden.

Conclusie?
Nee; voor een definitieve conclusie is het nog te vroeg, maar als ik mijn geld moet zetten op de keuzes tipping point of piramidespel gaat 99% op de laatste optie en 1% op de eerste. BranchOut biedt geen intrinsieke waarde maar lijkt simpelweg lang genoeg te hebben bestaan om in hogere aantallen van de expontentiele groeicurve te zijn aanbeland.

Als er inderdaad slechts sprake is van een piramidespel zal de zwaartekracht binnen afzienbare tijd haar onverbiddelijke wetmatigheid gaan tonen. En is er binnenkort een spectaculaire crash and burn te bewonderen… Een soort Jobster 2.0?